Динамика относительного движения. Динамика системы тел. Основные теоремы и понятия Общие теоремы динамики техническая механика
При большом количестве материальных точек, входящих в состав механической системы, или, если в её состав входят абсолютно твёрдые тела (), совершающие непоступательное движение, применение системы дифференциальных уравнений движения при решении основной задачи динамики механической системы оказывается практически неосуществимым. Однако при решении многих инженерных задач нет необходимости в определении движения каждой точки механической системы в отдельности. Иногда бывает достаточно сделать выводы о наиболее важных сторонах изучаемого процесса движения, не решая полностью систему уравнений движения. Эти выводы из дифференциальных уравнений движения механической системы составляют содержание общих теорем динамики. Общие теоремы, во-первых, освобождают от необходимости в каждом отдельном случае производить те математические преобразования, которые являются общими для разных задач и их раз и навсегда производят при выводе теорем из дифференциальных уравнений движения. Во-вторых, общие теоремы дают связь между общими агрегированными характеристиками движения механической системы, имеющими наглядный физический смысл. Эти общие характеристики, такие как количество движения, кинетический момент, кинетическая энергия механической системы называютсямерами движения механической системы.
Первая мера движения – количество движения механической системы
|
M k
|
Пусть
дана механическая система, состоящая
из
|
материальных точек
.Положение
каждой точки массой
определяется в инерциальной системе
отсчёта
радиус-вектором
(рис. 13.1).
Пусть
-
скорость точки
.Количеством движения материальной точки называется векторная мера её движения, равная произведению массы точки на её скорость:
.
Количеством движения механической системы называется векторная мера её движения, равная сумме количеств движения её точек:
, (13.1)
Преобразуем правую часть формулы (23.1):
где
-
масса всей системы,
-
скорость центра масс.
Следовательно, количество движения механической системы равно количеству движения её центра масс, если сосредоточить в нём всю массу системы:
.
Импульс силы
Произведение
силы на элементарный промежуток времени
её действия
называется элементарным импульсом
силы.
Импульсом
силы
за промежуток времени
называется интеграл от элементарного
импульса силы
.
Теорема об изменении количества движения механической системы
Пусть
на каждую точку
механической
системы действуют равнодействующая
внешних сил
и равнодействующая внутренних сил
.
Рассмотрим основные уравнения динамики механической системы
Складывая почленно уравнения (13.2) для n точек системы, получим
(13.3)
Первая
сумма в правой части равна главному
вектору
внешних сил системы. Вторая сумма равна
нулю по свойству внутренних сил системы.
Рассмотрим левую часть равенства (13.3):
Таким образом, получим:
, (13.4)
или в проекциях на оси координат
(13.5)
Равенства (13.4) и (13.5) выражают теорему об изменении количества движения механической системы:
Производная по времени от количества движения механической системы равна главному вектору всех внешних сил механической системы.
Эту теорему можно представить также в интегральной форме, проинтегрировав обе части равенства (13.4) по времени в пределах от t 0 до t :
, (13.6)
где
,
а интеграл в правой части – импульс
внешних сил за
время t -t 0 .
Равенство (13.6) представляет теорему в интегральной форме:
Приращение количества движения механической системы за конечное время равно импульсу внешних сил за это время.
Теорему называют также теоремой импульсов.
В проекциях на оси координат, теорема запишется в виде:
Следствия (законы сохранения количества движения)
1).
Если главный вектор внешних сил за
рассматриваемый промежуток времени
равен нулю, то количество движения
механической системы постоянно, т.е.
если
,
.
2). Если проекция главного вектора внешних сил на какую-либо ось за рассматриваемый промежуток времени равна нулю, то проекция количества движения механической системы на эту ось постоянна,
т.е.
если
то
.
Пусть материальная точка движется под действием силы F . Требуется определить движение этой точки по отношению к подвижной системе Oxyz (см. сложное движение материальной точки), которая движется известным образом по отношению к неподвижной системе O 1 x 1 y 1 z 1 .
Основное уравнение динамики в неподвижной системе
Запишем абсолютное ускорение точки по теореме Кориолиса
где a абс – абсолютное ускорение;
a отн – относительное ускорение;
a пер – переносное ускорение;
a кор – кориолисово ускорение.
Перепишем (25) с учетом (26)
Введем
обозначения
-
переносная сила инерции,
- кориолисова сила инерции. Тогда
уравнение (27)
приобретает вид
Основное уравнение динамики для изучения относительного движения (28) записывается как же как и для абсолютного движения, только к действующим на точку силам надо добавить переносную и кориолисову силы инерции.
Общие теоремы динамики материальной точки
При решении многих задач можно пользоваться выполненными заранее заготовками, полученными на основе второго закона Ньютона. Такие методы решения задач объединены в этом разделе.
Теорема об изменении количества движения материальной точки
Введем следующие динамические характеристики:
1. Количество движения материальной точки – векторная величина, равная произведению массы точки на вектор ее скорости
.
(29)
2. Импульс силы
Элементарный импульс силы – векторная величина, равная произведению вектора силы на элементарный промежуток времени
(30).
Тогда полный импульс
.
(31)
При F =const получим S =Ft .
Полный импульс за конечный промежуток времени можно вычислить только в двух случаях, когда действующая на точку сила постоянная или зависит то времени. В других случаях необходимо выразить силу как функцию времени.
Равенство размерностей импульса (29) и количества движения (30) позволяет установить между ними количественную взаимосвязь.
Рассмотрим движение материальной точки M под действием произвольной силы F по произвольной траектории.
О
УД:
.
(32)
Разделяем в (32) переменные и интегрируем
.
(33)
В итоге, принимая во внимание (31), получаем
.
(34)
Уравнение (34) выражает следующую теорему.
Теорема : Изменение количества движения материальной точки за некоторый промежуток времени равно импульсу силы, действующей на точку, за тот же интервал времени.
При решении задач уравнение (34) необходимо спроектировать на оси координат
Данной теоремой удобно пользоваться, когда среди заданных и неизвестных величин присутствуют масса точки, ее начальная и конечная скорость, силы и время движения.
Теорема об изменении момента количества движения материальной точки
М
омент
количества движения материальной точки
относительно центра равен произведению
модуля количества движения точки на
плечо, т.е. кратчайшее расстояние
(перпендикуляр) от центра до линии,
совпадающей с вектором скорости
,
(36)
.
(37)
Взаимосвязь между моментом силы (причиной) и моментом количества движения (следствием) устанавливает следующая теорема.
Пусть точка M заданной массы m движется под действием силы F .
,
,
,
(38)
.
(39)
Вычислим производную от (39)
.
(40)
Объединяя (40) и (38), окончательно получим
.
(41)
Уравнение (41) выражает следующую теорему.
Теорема : Производная по времени от вектора момента количества движения материальной точки относительно некоторого центра равна моменту действующей на точку силы относительно того же центра.
При решении задач уравнение (41) необходимо спроектировать на оси координат
В уравнениях (42) моменты количеств движения и силы вычисляются относительно координатных осей.
Из (41) вытекает закон сохранения момента количества движения (закон Кеплера).
Если момент силы, действующей на материальную точку, относительно какого-либо центра равен нулю, то момент количества движения точки относительно этого центра сохраняет свою величину и направление.
Если
,
то
.
Теорема и закон сохранения используются в задачах на криволинейное движение, в особенности при действии центральных сил.
Дифференциальные уравнения движения системы.
Применяем второй (основной) закон динамики, получим
Аналогичного вида уравнения получим для любой точки системы, т.е. всего для рассматриваемой системы будет иметь nтаких уравнений (k= 1, 2….n). Эта система уравнений представляет собойдифференциальные уравнения движения механической системы в векторной форме.
Проектируя равенства (2) на какие-нибудь координатные оси, получим систему дифференциальных уравнений движения системы в проекциях на эти оси.
В результате интегрирования системы дифференциальных уравнений (что очень сложно) получить законы движений каждой точки системы. Гораздо удобнее определять некоторые сумарные характеристики движения всей системы в целом, а по ним, если требуется, найти и соответствующие параметры движения отжельных точек системы.
Такими характеристиками являются меры движения системы: количество движения, момент количества движения, кинетическая инергия.
Приче м каждая из этих мер для системы определяется как сумма соответствующих мер движения всех ее точек.
Соответственно и воздействия на систему рассматриваются суммарно (главный вектор и главный момент приложенных к системе сил, суммы работ и т.п.).
Зависсимость между мерами движения системы и мерами воздействия на нее выражают общие теоремы системы материальных точек.
Общие теоремы динамики системы являются следствиями системы уравнений (2).
2) Масса системы. Центр масс.
Механическая система – это система материальных точек, каждая из которых имеет определенную массу и занимает в данный момент времени определенное положение в пространстве.
Для удобства решения задач динамики механические системы желательно некоторые обобщенные (т.е. суммарные) характеристики, которые бы отражали и массу системы, и ее «геометрию масс», т.е. расположение в пространстве материальных точек системы.
Масса системы М равна арифметической сумме масс всех точек или тел, образующих систему:
Центром масс механической системы называют геометрическую точку С, радиус вектор которой
где радиус- вектор точек, образующих систему.
Массы точек механической системы
М – масса системы.
Центр масс системы явл не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой системы. Центр масс системы характеризует распределение масс в системе.
Теорема о движении центра масс механической системы.
Теорема: Центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все действующие на систему внешние силы.
Где - ускорение центра масс.
Главный вектор внешних сил.
Проецируя обе части уравнения на координатные оси, получим:
где ,,- координаты центра масс.
Из теоремы о движения центра масс можно получить следующие важные следствия, которые выражают закон сохранения центра масс механической системы.
Если геометрическая система всех внешних сил, действующих на систему, равна 0 () то это значит, чтоили, т.е. центр масс этой системы движется с постоянной по модулю и направлению скоростью (иначе, равномерно и прямолинейно). В частном случае, если вначале центр масс был в покое () то он и останется в покое т.е ().
Если внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например, ось Х равна 0 , тоилит.е. проекция скорости центра масс системы на эту ось есть величина постоянная. В частном случае, если в начальный момент, то и в любой последующий момент времени это значение сохранится, а следовательно координатацентра масс системы не изменится т.е.=const.
Теоремы об изменении количества движения точки и системы
Определение: количеством движения материальной точки называется векторная величина ,равная произведению массы точки на вектор ее скорости. Векторприложен к движущейся точке.
Определение: Количеством движения механической системы называется вектор, равный геометрической сумме количеств движения всех точек системы.
Вектор является свободным вектором. Как правило скорости всех точек системы различны и поэтому непосредственное суммирование векторов в правой части равенства является затруднительным.
Воспользуемся формулой для определения центра масс механической системы (1)
Или запишем в виде
дифференциируя обе части выражения по времени получим:
Сравнивая формулы (4) и (5) получим, что количество движения системы равно произведению массы всей системы на скорость ее центра масс.
Вектор является обобщенной векторной характеристикой движения всей механической системы. В общем случае движение системы ее количество движения можно рассматривать как характеристику поступательной части движения системы вместе с центром масс. Если при движении системы (тела) центр масс неподвижен, то количество движения будет равно 0. Например количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс.
Запишем второй закон динамики для материальной точки: учитывая чтополучим(7)
В каждый момент времени производная по времени от количества движения точки равна действующей на точку силе.
Если обе части равенства (7) умножить на dt , то получимвекторная величина, стоящая в правой части этого равенства, характеризует действие, оказываемое на тело силой за элементарный промежуток времениdt эту величинуназывают элементарным импульсом силы, т.е.
Лекция 3. Общие теоремы динамики
Динамика системы материальных точек является важным разделом теоретической механики. Здесь в основном рассматриваются задачи о движении механических систем (систем материальных точек) с конечным числом степеней свободы – максимальным числом независимых параметров, определяющих положение системы. Главная задача динамики системы – изучение законов движения твердого тела и механических систем.
Наиболее простой подход к исследованию движения системы, состоящий из N материальных точек, сводиться к рассмотрению движений каждой отдельной точки системы. При этом должны быть определены все силы, действующие на каждую точку системы, в том числе и силы взаимодействия между точками.
Определяя ускорения каждой точки в соответствии со вторым законом Ньютона (1.2), получим для каждой точки три скалярных дифференциальных закона движения второго порядка, т.е. 3 N дифференциальных закона движения для всей системы.
Для нахождения уравнений движения механической системы по заданным силам и начальным условиям для каждой точки системы, полученные дифференциальные законы нужно проинтегрировать. Эта задача трудна даже в случае двух материальных точек, которые движутся только под действием сил взаимодействия по закону всемирного притяжения (задача о двух телах), и исключительно трудна в случае трех взаимодействующих точек (задача о трех телах).
Поэтому необходимо отыскать такие методы решения задач, которые бы приводили к решаемым уравнениям и давали представление о движении механической системы. Общие теоремы динамики, являясь следствием дифференциальных законов движения, позволяют избежать сложности, возникающие при интегрировании и получать необходимые результаты.
3. 1. Общие замечания
Точки механической системы будем нумеровать индексами i , j , k и т.д., которые пробегают все значения 1, 2, 3… N , где N – число точек системы. Физические величины, относящиеся к k -й точке, обозначаются таким же индексом, что и точка. Например, выражают соответственно радиус-вектор и скорость k -й точки.
На каждую из точек системы действуют силы двоякого происхождения: во-первых, силы, источники которых лежат вне системы, называемые внешними силами и обозначаемые ; во-вторых, силы со стороны других точек данной системы, называемые внутренними силами и обозначаемые . Внутренние силы удовлетворяют третьему закону Ньютона. Рассмотрим простейшие свойства внутренних сил, действующих на всю механическую систему в любом ее состоянии.
Первое свойство. Геометрическая сумма всех внутренних сил системы (главный вектор внутренних сил) равна нулю .
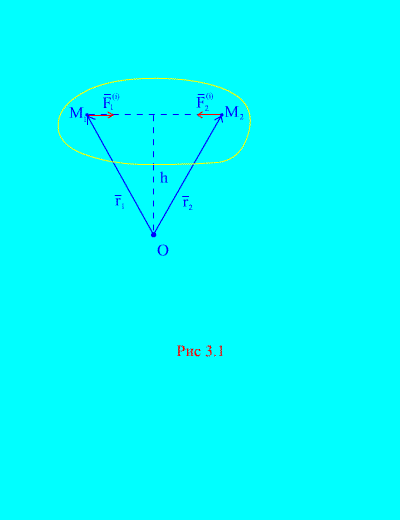
Действительно, если рассмотреть какие-либо две произвольные точки системы, например и (рис. 3.1)
, то для них 
, т.к. силы действия и противодействия всегда равны по модулю, действуют вдоль одной линии действия в противоположном направлении, которое соединяет взаимодействующие точки. Главный вектор внутренних сил состоит из пар сил взаимодействующих точек, следовательно
(3.1)
Второе свойство. Геометрическая сумма моментов всех внутренних сил относительно произвольной точки пространства равна нулю .
Рассмотрим систему моментов сил и относительно точки О (рис. 3.1) . Из (рис. 3.1) . видно, что
,
т.к. обе силы имеют одинаковые плечи и противоположные направления векторных моментов. Главный момент внутренних сил относительно точки О состоит из векторной суммы таких выражений и равен нулю. Следовательно,
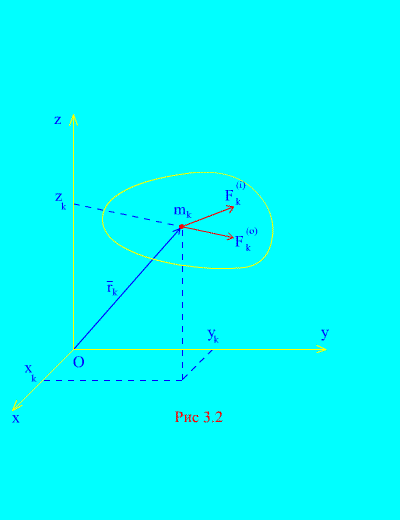
Пусть заданы внешние и внутренние силы, действующие на механическую систему, состоящую из N точек (рис. 3.2) . Если к каждой точке системы приложить равнодействующую внешних сил и равнодействующую всех внутренних сил , то для любой k -й точки системы можно составить дифференциальные уравнения движения. Всего таких уравнений будет N :
а в проекциях на неподвижные оси координат 3 N :
(3.4)
Векторные уравнения (3.3) или эквивалентные им скалярные уравнения (3.4) представляют дифференциальные законы движения материальных точек всей системы. Если все точки движутся параллельно одной плоскости или одной прямой, то число уравнений (3.4) в первом случае будет 2 N , во втором N .
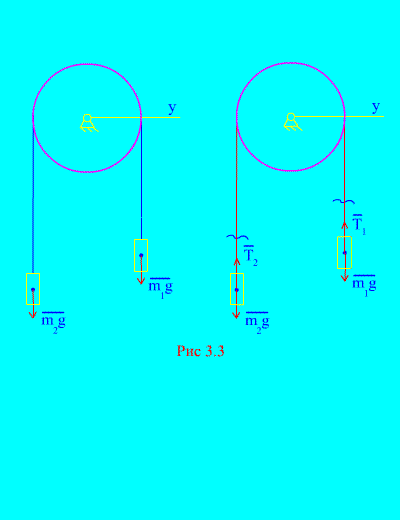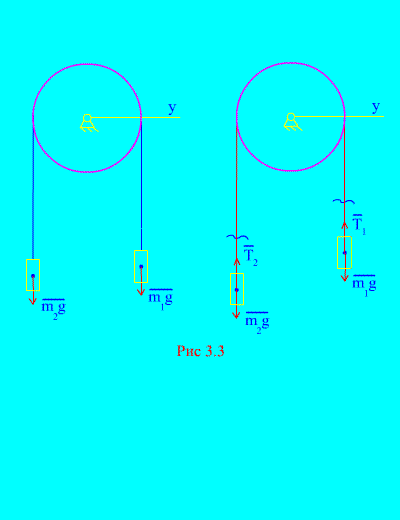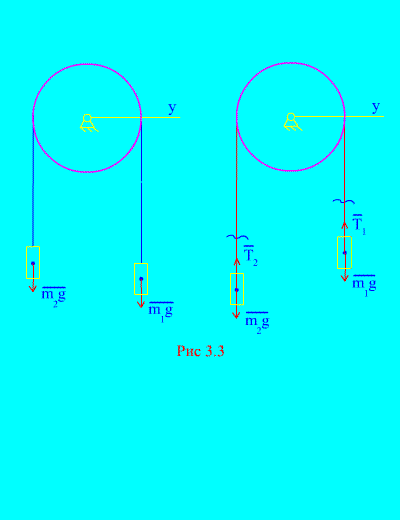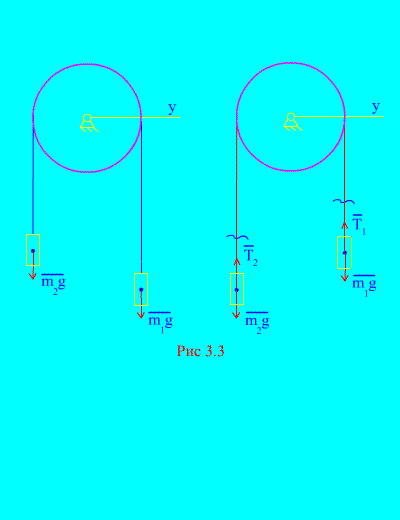
Пример 1. Два груза массой и связаны между собой нерастяжимым тросом, перекинутым через блок (рис. 3.3) . Пренебрегая силами трения, а также массой блока и троса, определить закон движения грузов и натяжения троса.
Решение . Система состоит из двух материальных тел (связанных нерастяжимым тросом), движущихся параллельно одной оси х. Запишем дифференциальные законы движения в проекциях на ось х для каждого тела.
Пусть правый груз опускается с ускорением , тогда левый груз будет подниматься с ускорением . Мысленно освобождаемся от связи (троса) и заменяем ее реакциями и (рис. 3.3) . Считая тела свободными, составим дифференциальные законы движения в проекции на ось х (имеется в виду, что натяжения нити являются внутренними силами, а вес грузов – внешними):
Поскольку и (тела связаны нерастяжимым тросом), получаем
Решая эти уравнения относительно ускорения и натяжения троса Т , получим
.
Отметим, что натяжение троса при не равно силе тяжести соответствующего груза.
3. 2. Теорема о движении центра масс
Известно, что твердое тело и механическая система в плоскости может двигаться достаточно сложно. К первой теореме о движении тела и механической системы можно прийти следующим образом: бросить к.-л. предмет, состоящий из множества скрепленных между собой твердых тел. Ясно, что он полетит по параболе. Это выявилось при изучении движения точки. Однако теперь объект не точка. Он поворачивается, покачивается в процессе полета вокруг некого эффективного центра, который движется по параболе. Первая теорема о движении сложных предметов говорит о том, что некий эффективный центр есть центр масс движущегося предмета. Центр масс не обязательно находится в самом теле, он может лежать и где-то вне его.
Теорема. Центр масс механической системы движется как материальная точка массой равной массе всей системы, к которой приложены все внешние силы, действующие на систему.
Для доказательства теоремы перепишем дифференциальные законы движения (3.3) в следующем виде:
(3.5)
где N – число точек системы.
Сложим почленно уравнения между собой:
(а)
Положение центра масс механической системы относительно выбранной системы координат определяется формулой (2.1): 
где М
– масса системы. Тогда левая часть равенства (а) запишется
Первая сумма, стоящая в правой части равенства (а), равна главному вектору внешних сил, а последняя по свойству внутренних сил равна нулю. Тогда равенство (а), с учетом (б) перепишется
, (3.6)
т.е. произведение массы системы на ускорение центра ее массы равно геометрической сумме всех действующих на систему внешних сил.
Из уравнения (3.6) следует, что внутренние силы непосредственно не влияют на движение центра масс. Однако в ряде случаев являются причиной появления внешних сил, приложенных к системе. Так, внутренние силы, приводящие во вращение ведущие колеса автомобиля, вызывают действие на него внешней силы сцепления, приложенной к ободу колеса.
Пример 2. Механизм, расположенный в вертикальной плоскости, установлен на горизонтальной гладкой плоскости и прикреплен к ней жестко закрепленными с поверхностью брусками К и L (рис. 3.4) .
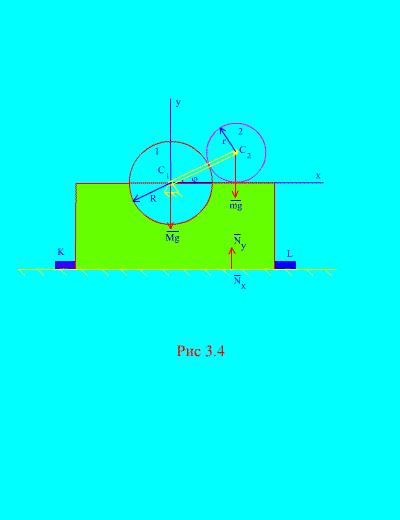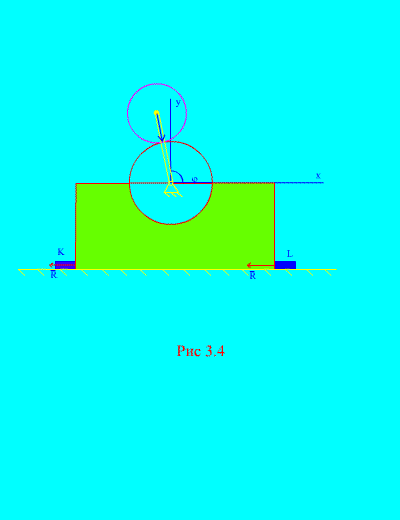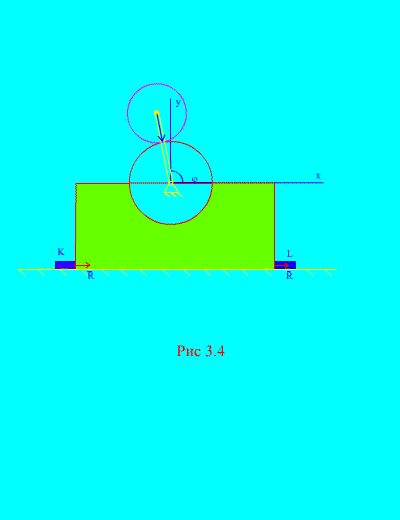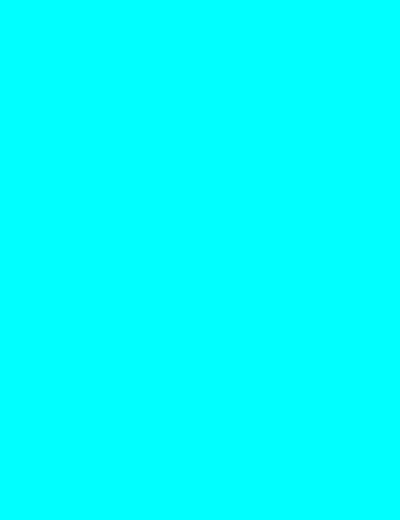
Диск 1 радиусом R неподвижен. Диск 2 массой m и радиусом r скреплен с кривошипом , длиной R + r в точке С 2 . Кривошип вращается с постоянной
угловой скоростью . В начальный момент кривошип занимал правое горизонтальное положение. Пренебрегая массой кривошипа, определить наибольшее горизонтальное и вертикальное усилия, действующие на бруски, если общая масса станины и колеса 1 равна М. Также рассмотреть поведение механизма при отсутствии брусков.
Решение . Система состоит из двух масс (N =2 ): неподвижного диска 1 со станиной и подвижного диска 2. Направим ось у через центр тяжести неподвижного диска по вертикали вверх, ось х – вдоль горизонтальной плоскости.
Запишем теорему о движении центра масс (3.6) в координатной форме
Внешними силами этой системы являются: вес станины и неподвижного диска – Mg , вес подвижного диска – mg , - суммарная горизонтальная реакция болтов, - нормальная суммарная реакция плоскости. Следовательно,
Тогда законы движения (б) перепишутся
Вычислим координаты центра масс механической системы:
; (г)
как видно из (рис. 3.4)
, , , 
(угол поворота кривошипа ), 
. Подставляя эти выражения в (г) и вычисляя вторые производные по времени t
от , , получим, что
(д)
Подставляя (в) и (д) в (б), находим
Горизонтальное давление, действующее на бруски, имеет наибольшее и наименьшее значения, когда cos = 1 соответственно, т.е
Давление механизма на горизонтальную плоскость имеет наибольшее и наименьшее значения, когда sin соответственно, т.е.
Фактически решена первая задача динамики: по известным уравнениям движения центра масс системы (д) восстанавливаются силы, участвующие в движении.
В условиях отсутствия брусков K и L (рис. 3.4) , механизм может начать подпрыгивать над горизонтальной плоскостью. Это будет иметь место, когда , т.е. когда , отсюда следует, что угловая скорость вращения кривошипа, при которой происходит подпрыгивание механизма, должна удовлетворять равенству
.
3. 3. Закон сохранения движения центра масс
Если главный вектор внешних сил, действующих на систему, равен нулю, т.е. , то из (3.6) следует, что ускорение центра масс равно нулю, следовательно, скорость центра масс является постоянной по модулю и направлению. Если, в частности, в начальный момент центр масс находится в покое, то он покоится в течение всего времени, пока главный вектор внешних сил равен нулю.
Из этой теоремы вытекает несколько следствий.
· Одними внутренними силами нельзя изменить характер движения центра масс системы.
· Если главный вектор внешних сил, действующих на систему, равен нулю, то центр масс находится в покое или движется равномерно и прямолинейно.
· Если проекция главного вектора внешних сил системы на некоторую неподвижную ось равна нулю, то проекция скорости центра масс системы на эту ось не изменяется.
· Пара сил, приложенная к твердому телу, не может изменить движение его центра масс (она может вызвать только вращение тела вокруг центра масс).
Рассмотрим пример, иллюстрирующий закон сохранения движения центра масс.
Пример 3. Два груза массами и соединены нерастяжимой нитью, переброшенной через блок (рис. 3.5) , закрепленный на клине массой М. Клин опирается на гладкую горизонтальную плоскость. В начальный момент система находилась в покое. Найти перемещение клина по плоскости при опускании первого груза на высоту Н. Массой блока и нити пренебречь.
Решение. Внешними силами, действующими на клин вместе с грузами, являются силы тяжести , и Mg , а также нормальная реакция гладкой горизонтальной поверхности N. Следовательно,
Поскольку в начальный момент система находилась в покое, имеем .
Вычислим координату центра масс системы при и в момент t 1 , когда груз весом g опустится на высоту H .
Для момента :
,
где , , х – соответственно координаты центра масс грузов весом g, g и клина весом М g .
Предположим, что клин в момент времени переместится в положительном направлении оси Ox на величину L , если груз весом опустится на высоту Н. Тогда, для момента
т.к. грузы вместе с клином передвинутся на L вправо, a груз переместится на расстояние по клину вверх. Так как , то после вычислений получим
.
3.4. Количество движения системы
3.4.1. Вычисление количества движения системы
Количеством движения материальной точки называется векторная величина, равная произведению массы точки на вектор ее скорости
Единица измерения количества движения -
Количеством движения механической системы называют векторную сумму количества движения отдельных точек системы, т.е.
где N – число точек системы.
Количество движения механической системы можно выразить через массу системы М и скорость центра масс . Действительно,
т.е. количество движения системы равно произведению массы всей системы на скорость ее центра масс. Направление совпадает с направлением (рис. 3.6)
В проекциях на прямоугольные оси имеем
где , , - проекции скорости центра масс системы.
Здесь М – масса механической системы; не меняется при движении системы.
Этими результатами особенно удобно пользоваться при вычислении количеств движения твердых тел.
Из формулы (3.7) видно, что если механическая система движется так, что ее центр масс остается неподвижным, то количество движения системы остается равным нулю.
3.4.2. Элементарный и полный импульс силы
Действие силы на материальную точку в течение времени dt можно охарактеризовать элементарным импульсом . Полный импульс силы за время t , или импульс силы , определяют по формуле
или в проекциях на координаты оси
(3.8а)
Единица импульса силы - .
3.4.3. Теорема об изменении количества движения системы
Пусть к точкам системы приложены внешние и внутренние силы. Тогда для каждой точки системы можно применить дифференциальные законы движения (3.3), имея в виду, что 
:
.
Суммируя по всем точкам системы, получим
По свойству внутренних сил и по определению 
имеем
(3.9)
Умножая обе части этого уравнения на dt , получим теорему об изменении количества движения в дифференциальной форме:
, (3.10)
т.е. дифференциал количества движения механической системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на точки механической системы.
Вычисляя интеграл от обеих частей (3.10) по времени от 0 до t , получим теорему в конечной или интегральной форме
(3.11)
В проекциях на координатные оси будем иметь
Изменение количества движения механической системы за время t , равно векторной сумме всех импульсов внешних сил, действующих на точки механической системы за то же время.
Пример 4. Груз массой m спускается вниз по наклонной плоскости из состояния покоя под действием силы F , пропорциональной времени: , где (рис. 3.7) . Какую скорость приобретет тело через t секунд после начала движения, если коэффициент трения скольжения груза о наклонную плоскость равен f .
Решение. Изобразим силы, приложенные к грузу: mg – сила тяжести груза, N – нормальная реакция плоскости, - сила трения скольжения груза о плоскость, причем . Направление всех сил изображено на (рис. 3.7) .
Направим ось х вдоль наклонной плоскости вниз. Запишем теорему об изменении количества движения (3.11) в проекции на ось х :
(а)
По условию , т.к. в начальный момент времени груз находился в состоянии покоя. Сумма проекций импульсов всех сил на ось х равна
Следовательно,
,
.
3.4.4. Законы сохранения количества движения
Законы сохранения получаются как частные случаи теоремы об изменении количества движения. Возможны два частных случая.
· Если векторная сумма всех внешних сил, приложенных к системе, равна нулю, т.е. , то из теоремы следует (3.9) , что ,
т.е. если главный вектор внешних сил системы равен нулю, то количество движения системы постоянно по величине и направлению.
· Если проекция главного вектора внешних сил на какую-либо координатную ось равна нулю, например Ох, т.е. , то проекция количества движения на эту ось величина постоянная .
Рассмотрим пример применения закона сохранения количества движения.
Пример 5. Баллистический маятник представляет собой тело массой , подвешенное на длинной нити (рис. 3.8) .
Пуля массой , движущаяся со скоростью V и попадающая в неподвижное тело, застревает в нем, и тело отклоняется. Какова была скорость пули, если тело поднялось на высоту h ?
Решение.
Пусть тело с застрявшей пулей приобрело скорость . Тогда, пользуясь законом сохранения количества движения при взаимодействии двух тел, можно записать 
.
Скорость можно вычислить, воспользовавшись законом сохранения механической энергии 
. Тогда . В результате находим
.
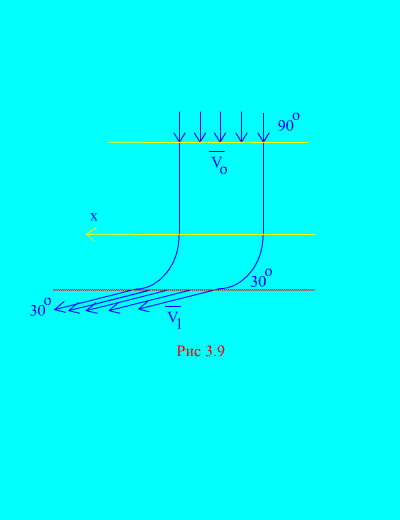
Пример 6 . Вода входит в неподвижный канал (рис. 3.9) переменного сечения со скоростью под углом к горизонту; площадь поперечного сечения канала при входе ; скорость воды у выхода из канала и составляет угол с горизонтом.
Определить горизонтальную составляющую реакции, которую вода оказывает на стенки канала. Плотность воды 
.
Решение. Будем определять горизонтальную составляющую реакции, оказываемой стенками канала на воду. Эта сила равна по модулю и противоположна по знаку искомой силе. Имеем, согласно (3.11а),
. (а)
Вычисляем массу объема жидкости, поступающей в канал за время t:
Величина rАV 0 называется секундной массой - масса жидкости, протекающей через любое сечение трубы в единицу времени.
Такое же количество воды покидает канал за это же время. Начальная и конечная скорости даны в условии.
Вычислим правую часть равенства (а) которая определяет сумму проекций на горизонтальную ось внешних сил, приложенных к системе (воде). Единственной горизонтальной силой является горизонтальная составляющая равнодействующей реакции стенок R x . Эта сила при установившемся движении воды является постоянной. Поэтому
. (в)
Подставляя (б) и (в) в (а), получаем
3.5. Кинетический момент системы
3.5.1. Главный момент количества движения системы
Пусть - радиус-вектор точки массой системы относительно некоторой точки А, называемой центром (рис. 3.10) .
Моментом количества движения (кинетическим моментом) точки относительно центра А называется вектор , определяемый по формуле
. (3.12)
При этом вектор направлен перпендикулярно плоскости, проходящей через центр А и вектор .
Моментом количества движения (кинетическим моментом) точки относительно оси называется проекция на эту ось момента количества движения точки относительно любого выбранного на данной оси центра.
Главным моментом количества движения (кинетическим моментом) системы относительно центра А называется величина
(3.13)
Главным моментом количества движения (кинетическим моментом) системы относительно оси называется проекция на эту ось главного момента количества движения системы относительно любого выбранного на данной оси центра.
3.5.2. Кинетический момент вращающегося твердого тела относительно оси вращения
Совместим неподвижную точку О тела, лежащую на оси вращения О z , с началом системы координат Оху z , оси которой будут вращаться вместе с телом (рис. 3.11) . Пусть - радиус-вектор точки тела относительно начала координат, его проекции на оси обозначим , , . Проекции вектора угловой скорости тела на те же оси обозначим 0, 0, ().
Теорема об изменении количества движения матер. точки . – количество движения материальной точки, – элементарный импульс силы. – элементарное изменение количества движения материальной точки равно элементарному импульсу силы, приложенной к этой точке (теорема в дифференц-ной форме) или – производная по времени от количества движения материальной точки равна равнодействующей сил, приложенных к этой точке. Проинтегрируем: – изменение количества движения материальной точки за конечный промежуток времени равно элементарному импульсу силы, приложенной к этой точке, за тот же промежуток времени. – импульс силы за промежуток времени . В проекциях на оси координат: и т.д.
Теорема об изменении момента количества движения матер. точки . - момент количества движения матер. точки относительно центра О. – производная по времени от момента количества движения матер. точки относительно какого-либо центра равна моменту силы, приложенной к точке, относительно того же центра. Проектируя векторное равенство на оси координат. получаем три скалярных уравнения: и т.д. - производная от момента кол-ва движения матер. точки относительно какой-либо оси равна моменту силы, приложенной к точке, относительно той же оси. При действии центральной силы, проходящей через О, М О = 0, Þ =const. =const, где – секторная скорость . Под действием центральной силы точка движется по плоской кривой с постоянной секторной скоростью, т.е. радиус-вектор точки описывает ("ометает") равные площади в любые равные промежутки времени (закон площадей) Этот закон имеет место при движении планет и спутников – один из законов Кеплера.
Работа силы. Мощность . Элементарная работа dA = F t ds, F t – проекция силы на касательную к траектории, направленная в сторону перемещения, или dA = Fdscosa.
Если a – острый, то dA>0, тупой – <0, a=90 o: dA=0. dA= – скалярное произведение вектора силы на вектор элементарного перемещения точки ее приложения; dA= F x dx+F y dy+F z dz – аналитическое выражение элементарной работы силы. Работа силы на любом конечном перемещении М 0 М 1: . Если сила постоянна , то = F×s×cosa. Единицы работы:.
Т.к. dx= dt и т.д., то .
Теорема о работе силы: Работа равнодействующей силы равна алгебраической сумме работ составляющих сил на том же перемещении А=А 1 +А 2 +…+А n .
Работа силы тяжести: , >0, если начальная точка выше конечной.
Работа силы упругости: –работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины.
Работа силы трения: если сила трения const, то - всегда отрицательна, F тр =fN, f – коэфф.трения, N – нормальная реакция поверхности.
Работа силы тяготения. Сила притяжения (тяготения): , из mg= , находим коэфф. k=gR 2 . – не зависит от траектории.
Мощность – величина, определяющая работу в единицу времени, . Если изменение работы происходит равномерно, то мощность постоянна : N=A/t. .
Теорема об изменении кинетической энергии точки . В диффер-ной форме: – полный дифференциал кинетической энергии мат.точки = элементарной работе всех действующих на точку сил. – кинетическая энергия матер.точки. В конечном виде: – изменение кинетической энергии мат.точки, при переходе ее из начального в конечное (текущее) положение равно сумме работ на этом перемещении всех сил, приложенных к точке.
Силовое поле – область, в каждой точке которой на помещенную в ней матер.точку действует сила, однозначно определенная по величине и направлению в любой момент времени, т.е. должно быть известна . Нестационарное силовое поле, если явно зависит от t, стационарное силовое поле, если сила не зависит от времени. Рассматриваются стационарные силовые поля, когда сила зависит только от положения точки: и F x =F x (x,y,z) и т.д. Свойства стационар. силовых полей:
1) Работа сил стац. поля зависит в общем случае от начального М 1 и конечного М 2 положений и траектории, но не зависит от закона движения матер. точки.
2) Имеет место равенство А 2,1 = – А 1,2 . Для нестационарных полей эти свойства на выполняются.
Примеры: поле силы тяжести, электростатическое поле, поле силы упругости.
Стационарные силовые поля, работа сил которых не зависит от траектории (пути) движения матер. точки и определяется только ее начальным и конечным положениями называется потенциальными (консервативными). , где I и II – любые пути, А 1,2 – общее значение работы. В потенциальных силовых полях существует такая функция, однозначно зависящая от координат точек системы, через которую проекции силы на координатные оси в каждой точке поля выражаются так:
Функция U=U(x 1 ,y 1 ,z 1 ,x 2 ,y 2 ,z 2 ,…x n ,y n ,z n) называется силовой функцией . Элементарная работа сил поля: dА=ådА i = dU. Если силовое поле является потенц-ным, элементарная работа сил в этом поле равна полному дифференциалу силовой функции. Работа сил на конечном перемещении , т.е. работа сил в потенц-ном поле равна разности значений силовой функции в конечном и начальном положениях и не зависит о формы траектории. На замкнутом перемещении работа равна 0. Потенциальная энергия П равна сумме работ сил потенциального поля на перемещении системы из данного положения в нулевое. В нулевом положении П 0 = 0. П=П(x 1 ,y 1 ,z 1 ,x 2 ,y 2 ,z 2 ,…x n ,y n ,z n). Работа сил поля на перемещении системы из 1-го положения во 2-ое равна разности потенциальных энергий А 1,2 = П 1 – П 2 . Эквипотенциальные поверхности – поверхности равного потенциала. Сила направлена по нормали к эквипотенциальной поверхности. Потенциальная энергия системы отличается от силовой функции, взятой со знаком минус, на постоянную величину U 0: А 1,0 = П =U 0 – U. Потенциальная энергия поля силы тяжести: П= mgz. Потенц.энерг.поля центральных сил. Центральная сила – сила, которая в любой точке пространства направлена по прямой, проходящей через некоторую точку (центр), и модуль ее зависит только от расстояния r точки массой m до центра: , . Центральной является гравитационная сила ,
F = 6,67×10 -11 м 3 /(кгс 2) – постоянная тяготения. Первая космическая скорость v 1 = » 7,9 км/с, R = 6,37×10 6 м – радиус Земли; тело выходит на круговую орбиту. Вторая космическая скорость: v 11 = » 11,2 км/с, траектория тела парабола, при v >v 11 – гипербола. Потенц. энергия восстанавливающей силы пружин:
L – модуль приращения длины пружины. Работа восстанавливающей силы пружины: , l 1 и l 2 – деформации, соответствующие начальной и конечной точкам пути.
Динамика материальной системы
Материальная система – совокупность материальных точек, движение которых взаимосвязаны. Масса системы = сумме масс всех точек (или тел), образующих систему: М=åm k . Центр масс (центр инерции) – геометрическая точка, радиус-вектор которой определяется равенством: , где – радиусы-векторы точек, образующих систему. Координаты центра масс: и т.д. Внешние силы F e – силы, действующие на точки системы со стороны тел, не входящих в систему. Внутренние силы F i – силы, вызванные взаимодействием точек, входящих в систему. Свойства внутренних сил: 1) Геометрическая сумма (главный вектор) всех внутренних сил = 0; 2) Геометрическая сумма моментов всех внутренних сил относительно произвольной точки = 0. Дифф-ные уравнения движения системы матер.точек :
Или в проекциях на оси координат: и т.д. для каждой точки (тела) системы. Геометрия масс .
Момент инерции матер.точки относительно некоторой оси называется произведение массы m этой точки на квадрат ее расстояния h до оси: mh 2 . Момент инерции тела (системы) относительно оси Оz: J z = åm k h k 2 . При непрерывном распределении масс (тело) сумма переходит в интеграл: J x = ò(y 2 +z 2)dm; J y = ò(z 2 +x 2)dm; J z = ò(x 2 +y 2)dm – относительно координатных осей. J z = M×r 2 , r – радиус инерции тела – расстояние от оси до точки в которой нужно сосредоточить всего тела, чтобы ее момент инерции равнялся моменту инерции тела. Момент инерции относительно оси (осевой момент инерции) всегда >0. Полярный момент инерции J o = ò(x 2 +y 2 +z 2)dm; J x +J y +J z = 2J o . Центробежный момент инерции J xy для матер.точки называется произведение ее координат x и y на ее массу m. Для тела центробежными моментами инерции называются величины, определяемые равенствами: J xy =òxy dm; J yz =òyz dm; J zx =òzx dm. Центробежные моменты инерции симметричны относительно своих индексов, т.е. J xy =J yx и т.д. В отличие от осевых, центробежные моменты инерции могут иметь любой знак и обращаться в нуль. Главной осью инерции тела называется ось, для которой оба центробежных момента инерции, содержащие индекс этой оси, равны нулю. Например, если J xz =J yz =0, то ось z – главная ось инерции. Главной центральной осью инерции называется главная ось инерции, проходящая через центр масс тела. 1)Если тело имеет плоскость симметрии, то любая ось, перпендикулярная к этой плоскости, будет главной осью инерции тела для точки, в которой ось пересекает плоскость. 2)Если тело имеет ось симметрии, то эта ось является главной осью инерции тела (ось динамической симметрии). Размерность всех моментов инерции [кгм 2 ]
Центробежный момент инерции зависят не только от направления координатных осей, но и от выбора начала координат.
Тензор инерции в данной точке:
Моменты инерции некоторых однородных тел:
стержень массы m и длины L: ; .
Однородный сплошной диск с центром в точке С радиуса R и массы m: . Полый цилиндр: ,
цилиндр с массой распределенной по ободу (обруч): .
Теорема Гюйгенса-Штейнера момент инерции тела относительно произвольной оси равен моменту инерции относительно оси ей параллельной и проходящей через центр масс тела плюс произведение массы тела на квадрат расстояния между осями:
Наименьший момент инерции будет относительно той оси, которая проходит через центр масс. Момент инерции относительно произвольной оси L: J = J x cos 2 a + J y cos 2 b + J z cos 2 g – 2J xy cosacosb – 2J yz cosbcosg – 2J zx cosgcosa,
если координатные оси являются главными относительно своего начала, то:
J = J x cos 2 a + J y cos 2 b + J z cos 2 g. Теорема о движении центра масс системы.
Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил – дифференциальное уравнение движения центра масс. В проекциях на оси координат: .
Закон сохранения движения центра масс . Если главный вектор (векторная сумма) внешних сил остается все время равным нулю, то центр масс механической системы находится в покое или движется прямолинейно и равномерно. Аналогично в проекциях на оси, если Þ , если при этом в начальный момент v Cx 0 = 0, то Þ Þ x C = const.
Количество движения системы Q (иногда обозначают К) – вектор, равный геометрической сумме (главному вектору) количеств движения всех точек системы:
М – масса всей системы, v C – скорость центра масс.
Теорема об изменении количества движения системы: – производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил, действующих на эту систему. В проекциях: , и т.д. Теорема об изменении кол-ва движения системы в интегральной форме:
Где – импульсы внешних сил .
В проекциях: Q 1 x – Q 0 x = åS e kx и т.д. количество движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени. Закон сохранения количества движения – если сумма всех внешних сил, действующих на систему, = 0, то вектор количества движения системы будет постоянен по модулю и направлению: Þ = const, аналогично в проекциях: Þ Q x = const. Из закона следует, что внутренние силы изменить суммарное количество движение системы не могут. Тело переменной массы , масса которого непрерывно изменяется с течением времени m= f(t) (пр.: ракета, топливо которой убывает). Дифф-ное уравнение движения точки переменной массы:
– уравнение Мещерского , u – относительная скорость отделяющихся частиц. – реактивная сила, - секундный расход топлива, . Реактивная сила направлена в противоположную сторону относительной скорости истечения топлива.
Формула Циолковского : - определяет скорость ракеты, когда все топливо будет израсходовано – скорость в конце активного участка, m т – масса топлива, m k – масса корпуса ракеты, v 0 – начальная скорость. – число Циолковского, m 0 – стартовая масса ракеты. От режима работы ракетного двигателя, т.е. от того насколько быстро сжигается топливо, скорость ракеты в конце периода горения не зависит. Для достижения 1-ой космической скорости 7,9 км/с, при m 0 /m k = 4, скорость отброса должна быть 6 км/с, что трудно осуществить, поэтому применяются составные (многоступенчатые) ракеты.
Главный момент количеств движения матер. системы (кинетический момент) – величина, равная геометрической сумме моментов количеств движения всех точек системы относительно центра О. . Теорема об изменении момента количеств движения системы (теорема об изменении кинетического момента) :
Производная по времени от кинетического момента механич. системы относительно некоторого неподвижного центра геометрически равна главному моменту внешних сил, действующих на эту систему относительно того же центра. Аналогичные равенства относительно осей координат: и т.д.
Закон сохранения кинетического момента: если , то . Главный момент количеств движения системы является характеристикой вращательного движения. Кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела: K z = J z w. Если M z = 0, то J z w = const, J z – момент инерции тела..
Кинетическая энергия системы – скалярная величина Т, равная арифметической сумме кинетической энергий всех точек системы: . Если система состоит из нескольких тел, то Т = åТ к. Поступательное движение: Т пост = ,. Вращательное движ-ие: Т вр = , J z – момент инерции относительно оси вращения. Плоскопараллельное (плоское) движ-ие: Т пл = + , v C – скорость центра масс. Общий случай: Т= + , J CP – момент инерции тела относительно мгновенной оси. Теорема Кенига: Т= + – кинетич. энергия мех. сист. = сумме кинетич. энергии центра масс системы, масса которого равна массе всей системы, и кинетич. энергии этой системы в ее относительном движении относительно центра масс. Работа силы: , работа момента: . Мощность: N= Fv, N=M z w. Теорема об изменении кинетической энергии системы : в дифференциальной форме: dT = , , – элементарные работы, действующих на точку внешних и внутренних сил, в конечной форме:
Т 2 – Т 1 = . Для неизменяемой системы и Т 2 – Т 1 = , т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении. Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называются идеальными. Коэффициент полезного действия (кпд): < 1, А пол.сопр. – работа полезных сил сопротивления (сил, для которых предназначена машина), А затр = А пол.сопр. + А вр.сопр. – затраченная работа, А вр.сопр. -– работа вредных сил сопротивления (силы трения, сопротивления воздуха и т.п.).
h= N маш /N дв, N маш – полезная мощность машины, N дв – мощность дв-ля, приводящего ее в движение. Закон сохранения полной механической энергии : Т + П = const. Если система движется под действием потенциальных сил, то сумма кинетической и потенциальной энергий сохраняет постоянное значение. (Т + П - интеграл энергии). Потенциальные силы – силы, работа которых не зависит от вида траектории, по которой перемещается точка (пр.: сила тяжести, сила упругости) Непотенциальные – напр.: силы трения. Механическая энергия – сумма кинетической и потенциальной энергий. Расход механической энергии обычно означает превращение ее в теплоту, электричество, звук или свет, а приток механической энергии связан с обратным процессом превращения различных видов энергии в механическую энергию.
Динамика твердого тела
Дифференциальные уравнения поступательного движения твердого тела: и т.д. – проекция внешней силы. Все точки тела движутся так же, как и его центр масс С. Для осуществления поступательного движения необходимо, чтобы главный момент всех внешних сил относительно центра масс был равен 0: =0.
Дифф-ные уравнения вращения твердого тела вокруг неподвижной оси : ,
J z – момент инерции тела относительно оси вращения z, – момент внешних сил относительно оси вращения (вращающий момент). , e – угловое ускорение, чем больше момент инерции при данном , тем меньше ускорение, т.е момент инерции при вращательном движении является аналогом массы при поступательном. Зная , можно найти закон вращения тела j=f(t), и, наоборот, зная j=f(t), можно найти момент. Частные случаи: 1) если = 0, то w = const – тело вращается равномерно; 2) = const, то e = const – вращение равнопеременное. Уравнение аналогичное дифф-ному уравнению прямолинейного движения точки .
Физический маятник – твердое тело, совершающее колебания вокруг неподвижной горизонтальной оси под действием силы тяжести. Ур-ние вращательного движения:
Обозначая , получаем дифф-ное уравнение колебаний маятника: , k – частота колебаний маятника. Рассматривая малые колебания, можно считать sinj » j, тогда – дифф-ное уравнение гармонических колебаний. Решение этого уравнения: j = С 1 coskt + C 2 sinkt или j = asin(kt + b), a – амплитуда колебаний маятника, b – начальная фаза колебаний. Период малых колебаний физического маятника Т= 2p/k = 2p . Для малых колебаний маятника период не зависит от угла начального отклонения, этот результат является приближенным. Для математического маятника (материальной точки, подвешенной на нерастяжимой нити и движущейся под действием силы тяжести) имеем дифф. уравнения движения:
L – длина нити. Если L= , то математический маятник будет двигаться так же, как и физический (период колебаний совпадает). Величина L назыв-ся приведенной длиной физического маятника. Точка К, отстоящая от оси подвеса на расстоянии ОК=L, назыв-ся центром качаний физич. маятника. Если ось подвеса взять в точке К, то точка О будет центром качаний и наоборот – свойство взаимности . Расстояние ОК всегда >ОС, т.е. центр качаний всегда расположен ниже центра масс.
Динамика плоского движения твердого тела
Положение тела определяется положением полюса и углом поворота тела вокруг полюса. Дифф-ные уравнения плоского движения тв. тела :
; ; , С – центр масс тела, J C – момент инерции тела относительно оси, перпендикулярной плоскости движения тела и проходящей через его центр масс.
Принцип Даламбера (метод кинетостатики)
В каждый момент движения сумма активных сил, реакций связей и сил инерции равна нулю - принцип Даламбера для материальной точки.
– внешняя сила, – внутренняя сила. Сила инерции: , знак (–) показывает, что сила инерции направлена в противоположную сторону ускорению.
Для системы добавляется уравнение моментов: .
Обозначают: – главный вектор сил инерции, – главный момент сил инерции. Учитывая, что геометрическая сумма внутренних сил и сумма их моментов равна нулю , , получаем: , - уравнения кинетостатики. Принцип Даламбера для системы – если в любой момент времени к каждой точке системы приложить, кроме реально действующих сил, соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно применять уравнения статики. Это упрощает процесс решения задач.
Главный вектор сил инерции равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.
Главный момент сил инерции зависит от вида движения: при поступательном движении ; при плоском , при вращении вокруг оси z, проходящей через центр масс тела, .
Условия отсутствия динамических составляющих :
Откуда
x C = 0, y C = 0, J yz = 0, J zx = 0, это означает, что центр тяжести должен находиться на оси вращения тела и ось вращения тела z должна быть главной осью инерции тела. Т.е. ось вращения должна являться главной центральной осью инерции тела (ось, которая проходит через центр масс тела, и центробежные моменты инерции с индексом этой оси равны нулю). Для выполнения этого условия проводится специальная балансировка быстро вращающихся тел.
Основы аналитической механики
Возможные (виртуальные) перемещения системы (ds, dj) – любая совокупность бесконечно малых перемещений точек системы, допускаемых в данный момент наложенными на систему связями. Возможные перемещения рассматривают как величины первого порядка малости, пренебрегая при этом величинами высших порядков малости. Т.е. криволинейные перемещения точек заменяют прямолинейными отрезками, отложенными по касательным к их траекториям.
Число независимых между собою возможных перемещений системы называется числом степеней свободы этой системы. Например. шар на плоскости может перемещаться в любом направлении, но любое его возможное перемещение может быть получено как геометрическая сумма двух перемещений вдоль двух взаимно перпендикулярных осей. Свободное твердое тело имеет 6 степеней свободы.
Возможная (виртуальная) работа dА – элементарная работа, которую, действующая на матер.точку сила могла бы совершить на возможном перемещении этой точки.
Связи являются идеальными , если сумма элементарных работ реакций этих связей при любом возможном перемещении системы равна нулю, т.е. SdА r =0.
Принцип возможных перемещений : для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении была равна нулю. или в проекциях: .
Принцип возможных перемещений дает в общей форме условия равновесия для любой механической системы, дает общий метод решения задач статики.
Если система имеет несколько степеней свободы, то уравнение принципа возможных перемещений составляют для каждого из независимого перемещений в отдельности, т.е. будет столько уравнений, сколько система имеет степеней свободы.
Общее уравнение динамики – при движении системы с идеальными связями в каждый данный момент времен сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю. Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы. Дает общий метод решения задач динамики. Последовательность составления: а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные перемещения; в) составляют уравнения принципа возможных перемещений, считая систему находящейся в равновесии.
Уравнения Лагранжа 2-го рода : , (i=1,2…s) – дифференциальные уравнения второго порядка, s – число степеней свободы системы (число независимых координат); q i – обобщенная координата (перемещение, угол, площадь и др.); – обобщенная скорость (линейная скорость, угловая, секторная и др.),
Т = Т(q 1 ,q 2 ,…,q S , , … ,t) – кинетическая энергия системы, Q i – обобщенная сила (сила, момент и др.), ее размерность зависит от размерности обобщенной координаты и размерности работы.
Для вычисления обобщенной силы, например Q 1 , задаем возможное перемещение, при котором все вариации обобщенных координат, кроме dq 1 , равны нулю:
dq 1 ¹0, dq 2 = dq 3 =…= dq S = 0. Вычисляем на этом перемещении возможную работу dА 1 всех активных сил, приложенных к системе. Имея dА 1 = Q 1 dq 1 , находим .
