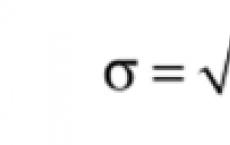Caractéristique de dispersion. Caractéristiques de la distribution statistique. Qualité de surface obtenue par roulement à billes. Diagramme de processus, valeur de pression, fréquence d'application de la force de déformation, équipement technologique dans les processus
Quelle que soit l'importance des caractéristiques moyennes, une caractéristique tout aussi importante du tableau de données numériques est le comportement des membres restants du tableau par rapport à la moyenne, à quel point ils diffèrent de la moyenne, combien de membres du tableau diffèrent. significativement par rapport à la moyenne. Dans l'entraînement au tir, ils parlent de la précision des résultats, dans les statistiques, ils étudient les caractéristiques de la dispersion (spread).
La différence entre toute valeur de x, à partir de la valeur moyenne de x est appelée déviation et calculé comme la différence x, - x. Dans ce cas, l'écart peut prendre à la fois des valeurs positives, si le nombre est supérieur à la moyenne, et des valeurs négatives, si le nombre est inférieur à la moyenne. Cependant, en statistique, il est souvent important de pouvoir opérer avec un nombre qui caractérise la «précision» de tous les éléments numériques du tableau de données. Toute sommation de tous les écarts des membres du tableau se traduira par zéro, car les écarts positifs et négatifs s'annuleront. Pour éviter la remise à zéro, les différences au carré sont utilisées pour caractériser la diffusion, plus précisément la moyenne arithmétique des écarts au carré. Cette caractéristique de diffusion est appelée la variance de l'échantillon.
Plus la variance est grande, plus la dispersion des valeurs de la variable aléatoire est grande. Pour calculer la variance, une valeur approximative de la moyenne de l'échantillon x est utilisée avec une marge d'un chiffre par rapport à tous les membres du tableau de données. Sinon, lors de la somme d'un grand nombre de valeurs approximatives, une erreur significative s'accumule. En ce qui concerne la dimension des valeurs numériques, il convient de noter un inconvénient d'un indicateur de diffusion tel que la variance de l'échantillon: l'unité de mesure de la variance ré est l'unité au carré des valeurs x, la caractéristique dont la variance est. Pour se débarrasser de cet inconvénient, les statistiques ont introduit une caractéristique de diffusion telle que écart type de l'échantillon , qui est désigné par le symbole et (lire "sigma") et est calculé par la formule

Normalement, plus de la moitié des membres de l'ensemble de données diffèrent de la moyenne de moins que la valeur de l'écart type, c'est-à-dire appartiennent au segment [X - et; x + a]. Sinon, disent-ils: la moyenne, compte tenu de l'étalement des données, est égale à x ± a.
L'introduction d'une autre caractéristique de diffusion est associée à la dimension des membres du tableau de données. Toutes les caractéristiques numériques des statistiques sont introduites afin de comparer les résultats de recherche de différents tableaux numériques caractérisant différentes variables aléatoires. Cependant, la comparaison des écarts-types de différentes valeurs moyennes de différents ensembles de données n'est pas indicative, surtout si la dimension de ces valeurs est également différente. Par exemple, lors de la comparaison de la longueur et du poids de tout objet ou de la dispersion dans la fabrication de micro et macro produits. En relation avec les considérations ci-dessus, une caractéristique de diffusion relative est introduite, appelée coefficient de variationet est calculé par la formule
Pour calculer les caractéristiques numériques de la diffusion des valeurs d'une variable aléatoire, il convient d'utiliser le tableau (tableau 6.9).
Tableau 6.9
Calcul des caractéristiques numériques de la diffusion des valeurs d'une variable aléatoire
|
Xj- X |
(Xj-X) 2 / |
||||
Lors du remplissage de ce tableau, la moyenne de l'échantillon est trouvée x,qui sera ensuite utilisé sous deux formes. En tant que caractéristique moyenne finale (par exemple, dans la troisième colonne du tableau), la moyenne de l'échantillon x doit être arrondi au bit le plus bas de tout membre d'un tableau de données numériques x g Cependant, cet indicateur est utilisé dans le tableau pour des calculs ultérieurs, et dans cette situation, à savoir, lors du calcul dans la quatrième colonne du tableau, la moyenne de l'échantillon x doit être arrondie à une marge d'un chiffre par rapport au plus petit chiffre de tout membre d'un tableau de données numériques x (.
Le résultat des calculs utilisant une table telle qu'une table. 6.9 obtiendra la valeur de la variance de l'échantillon, et pour enregistrer la réponse, il est nécessaire de calculer la valeur de l'écart type a sur la base de la valeur de la variance de l'échantillon.
La réponse indique: a) le résultat moyen, en tenant compte de la diffusion des données sous la forme x ± o; b) caractéristique de la stabilité des données V. Dans la réponse, la qualité du coefficient de variation doit être évaluée: bonne ou mauvaise.
Le coefficient de variation acceptable comme indicateur de l'uniformité ou de la stabilité des résultats de la recherche sportive est de 10 à 15%. Le coefficient de variation V \u003d 20% dans toute recherche est considéré comme un très grand indicateur. Si la taille de l'échantillon p \u003e 25, puis V> 32% est un très mauvais indicateur.
Par exemple, pour une série de variations discrètes 1; cinq; quatre; quatre; cinq; 3; 3; une; une; une; une; une; une; 3; 3; cinq; 3; cinq; quatre; quatre; 3; 3; 3; 3; 3 onglet. 6.9 sera rempli comme suit (Tableau 6.10).
Tableau 6.10
Un exemple de calcul des caractéristiques numériques de la dispersion des valeurs
|
*1 |
fi |
||||
|
1 |
|||||
|
L p 25 = 2,92 = 2,9 |
D _S_47.6_ p 25 |
Répondre: a) la caractéristique moyenne, compte tenu de la dispersion des données, est égale à x ± a \u003d \u003d 3 ± 1,4; b) la stabilité des mesures obtenues est à un niveau bas, puisque le coefficient de variation V = 48% > 32%.
Table analogique. 6.9 peut également être utilisé pour calculer les caractéristiques de diffusion d'une série de variations d'intervalle. De plus, les options x g sera remplacé par des représentants des lacunes x v ja option de fréquences absolues f (- pour les fréquences absolues des écarts f v
Sur la base de ce qui précède, ce qui suit peut être fait résultats.
Les conclusions des statistiques mathématiques sont plausibles si des informations sur les phénomènes de masse sont traitées.
Habituellement, un échantillon de la population générale d'objets est examiné, qui doit être représentatif.
Les données expérimentales obtenues à la suite de l'étude de toute propriété des objets de l'échantillon représentent la valeur d'une variable aléatoire, car le chercheur ne peut pas prédire à l'avance quel nombre correspondra à un certain objet.
Pour sélectionner l'un ou l'autre algorithme de description et de traitement primaire des données expérimentales, il est important de pouvoir déterminer le type de variable aléatoire: discrète, continue ou mixte.
Les variables aléatoires discrètes sont décrites par une série de variations discrètes et sa forme graphique - un polygone de fréquences.
Les variables aléatoires mixtes et continues sont décrites par une série de variations d'intervalle et sa forme graphique - un histogramme.
Lors de la comparaison de plusieurs échantillons par le niveau du ™ généré d'une certaine propriété, les caractéristiques numériques moyennes et les caractéristiques numériques de la diffusion d'une variable aléatoire par rapport à la moyenne sont utilisées.
Lors du calcul de la caractéristique moyenne, il est important de choisir le type correct de caractéristique moyenne qui convient à son domaine d'application. Les valeurs structurelles moyennes du mod et de la médiane caractérisent la structure de l'emplacement du variant dans le tableau ordonné de données expérimentales. La moyenne quantitative permet de juger de la taille moyenne du variant (moyenne de l'échantillon).
Pour calculer les caractéristiques numériques de la diffusion - variance de l'échantillon, écart type et coefficient de variation - la méthode tabulaire est efficace.
Les caractéristiques de position décrivent le centre de la distribution. Dans le même temps, les valeurs d'une variante peuvent être regroupées autour d'elle dans une bande large et étroite. Par conséquent, pour décrire la distribution, il est nécessaire de caractériser la plage de variation des valeurs caractéristiques. Les caractéristiques de diffusion sont utilisées pour décrire la plage de variation de l'entité. Les plus largement utilisés sont la plage de variation, la variance, l'écart type et le coefficient de variation.
Variation de balayage est définie comme la différence entre la valeur maximale et minimale d'un trait dans la population étudiée:
R=x max - x min.
L'avantage évident de l'indicateur considéré est la simplicité du calcul. Cependant, comme la plage de variation dépend des valeurs des seules valeurs extrêmes de la caractéristique, la portée de son application est limitée à des distributions assez uniformes. Dans d'autres cas, la valeur informative de cet indicateur est très faible, car il existe de nombreuses distributions de forme très différente, mais ayant la même plage. Dans les études pratiques, la plage de variation est parfois utilisée pour des échantillons de petite taille (pas plus de 10). Ainsi, par exemple, par la gamme de variation, il est facile d'évaluer la différence entre les meilleurs et les pires résultats dans un groupe d'athlètes.
Dans cet exemple:
R\u003d 16,36 - 13,04 \u003d 3,32 (m).
La deuxième caractéristique de la diffusion est dispersion. La variance est le carré moyen de l'écart de la valeur d'une variable aléatoire par rapport à sa moyenne. La dispersion est une caractéristique de la diffusion, la dispersion des valeurs d'une grandeur autour de sa valeur moyenne. Le mot même «dispersion» signifie «dispersion».
Lors de la réalisation d'études par sondage, il est nécessaire d'établir une estimation de la variance. La variance calculée à partir des données d'échantillon est appelée variance d'échantillon et est notée S 2 .
À première vue, l'estimation la plus naturelle de la variance est la variance statistique, calculée en fonction de la définition, selon la formule:
Dans cette formule, la somme des carrés des écarts des valeurs caractéristiques x ià partir de la moyenne arithmétique . Pour obtenir le carré moyen des écarts, cette somme est divisée par la taille de l'échantillon p.
Cependant, cette estimation n'est pas impartiale. On peut montrer que la somme des carrés des écarts des valeurs d'attribut pour la moyenne arithmétique de l'échantillon est inférieure à la somme des carrés des écarts par rapport à toute autre valeur, y compris la moyenne vraie (espérance mathématique). Par conséquent, le résultat obtenu par la formule ci-dessus contiendra une erreur systématique et la valeur estimée de la variance sera sous-estimée. Pour éliminer le biais, il suffit de saisir un facteur de correction. Le résultat est la relation suivante pour la variance estimée:
Pour les grandes valeurs nNaturellement, les deux estimations - biaisées et non biaisées - différeront très peu et l'introduction du facteur de correction perdra de son sens. En règle générale, l'affinement de la formule d'estimation de la variance doit être effectué lorsque n<30.
Dans le cas de données groupées, la dernière formule peut être réduite à la forme suivante pour simplifier les calculs:
où k - le nombre d'intervalles de regroupement;
n je - fréquence d'intervalle avec nombre je;
x i- la valeur médiane de l'intervalle avec le nombre je.
À titre d'exemple, calculons la variance des données groupées de l'exemple que nous analysons (voir tableau 4.):
S 2 =/ 28 \u003d 0,5473 (m2).
La variance d'une variable aléatoire a la dimension du carré de la dimension de la variable aléatoire, ce qui complique son interprétation et la rend peu claire. Pour une description plus visuelle de la diffusion, il est plus pratique d'utiliser une caractéristique dont la dimension coïncide avec la dimension de l'attribut étudié. A cet effet, le concept est introduit écart-type (ou écart-type).
Écart-type appelé la racine carrée positive de la variance:
Dans notre exemple, l'écart type est
L'écart type a les mêmes unités de mesure que les résultats de mesure de l'entité étudiée et, par conséquent, il caractérise le degré d'écart de l'entité par rapport à la moyenne arithmétique. En d'autres termes, il montre comment se situe la partie principale de la variante par rapport à la moyenne arithmétique.
L'écart type et la variance sont les mesures de variation les plus largement utilisées. Cela est dû au fait qu'ils sont inclus dans une partie importante des théorèmes de la théorie des probabilités, qui sert de fondement à la statistique mathématique. De plus, la variance peut être décomposée en ses éléments constitutifs, qui permettent d'évaluer l'influence de différents facteurs sur la variation du trait étudié.
En plus des indicateurs absolus de variation, que sont la variance et l'écart type, des valeurs relatives sont saisies dans les statistiques. Le coefficient de variation est le plus couramment utilisé. Le coefficient de variation est égal au rapport de l'écart type à la moyenne arithmétique, exprimé en pourcentage:
Il ressort clairement de la définition que, dans son sens, le coefficient de variation est une mesure relative de la dispersion d'un élément.
Pour l'exemple en question:
Le coefficient de variation est largement utilisé dans la recherche statistique. En tant que valeur relative, il vous permet de comparer les fluctuations des deux entités qui ont des unités de mesure différentes, et la même entité dans plusieurs populations différentes avec des valeurs différentes de la moyenne arithmétique.
Le coefficient de variation permet de caractériser l'homogénéité des données expérimentales obtenues. Dans la pratique de la culture physique et du sport, la dispersion des résultats de mesure en fonction de la valeur du coefficient de variation est considérée comme faible (V<10%), средним (11-20%) и большим (V> 20%).
Les restrictions sur l'utilisation du coefficient de variation sont liées à sa nature relative - la définition contient une normalisation à la moyenne arithmétique. À cet égard, à de petites valeurs absolues de la moyenne arithmétique, le coefficient de variation peut perdre son contenu informatif. Plus la valeur de la moyenne arithmétique est proche de zéro, moins cet indicateur devient informatif. Dans le cas limite, la moyenne arithmétique vire à zéro (par exemple, température) et le coefficient de variation passe à l'infini, quel que soit l'étalement du trait. Par analogie avec le cas d'erreur, la règle suivante peut être formulée. Si la valeur de la moyenne arithmétique dans l'échantillon est supérieure à un, alors l'utilisation du coefficient de variation est légitime; sinon, la variance et l'écart type doivent être utilisés pour décrire la dispersion des données expérimentales.
En conclusion de cette partie, nous considérerons l'évaluation de la variation des valeurs des caractéristiques estimées. Comme déjà noté, les valeurs des caractéristiques de distribution calculées à partir des données expérimentales ne coïncident pas avec leurs valeurs réelles pour la population générale. Il n'est pas possible d'établir précisément ce dernier car, en règle générale, il est impossible d'enquêter sur l'ensemble de la population générale. Si nous utilisons les résultats de différents échantillons de la même population générale pour estimer les paramètres de distribution, il s'avère que ces estimations pour différents échantillons diffèrent les unes des autres. Les valeurs estimées fluctuent autour de leurs vraies valeurs.
Les écarts des estimations des paramètres généraux par rapport aux valeurs réelles de ces paramètres sont appelés erreurs statistiques. La raison de leur apparition est la taille limitée de l'échantillon - tous les objets de la population générale n'y sont pas inclus. Pour estimer l'ampleur des erreurs statistiques, l'écart type des caractéristiques de l'échantillon est utilisé.
À titre d'exemple, considérons la caractéristique de position la plus importante - la moyenne arithmétique. On peut montrer que l'écart type de la moyenne arithmétique est déterminé par le rapport:
où σ est l'écart type de la population générale.
La valeur réelle de l'écart type n'étant pas connue, une quantité appelée erreur standard de la moyenne arithmétique et égal:
La valeur caractérise l'erreur qui, en moyenne, est autorisée lorsque la moyenne générale est remplacée par son estimation d'échantillon. Selon la formule, une augmentation de la taille de l'échantillon au cours de l'étude entraîne une diminution de l'erreur type proportionnellement à la racine carrée de la taille de l'échantillon.
Pour cet exemple, la valeur de l'erreur standard de la moyenne arithmétique est égale à. Dans notre cas, il s'est avéré être 5,4 fois inférieur à l'écart type.
but du travail
Familiarisez-vous avec le phénomène de diffusion et apprenez à en déterminer les caractéristiques.
Équipement
1. Disques avec une valeur nominale ET 1 .
2. Disques avec valeur nominale ET 2 .
3. Micromètre.
4. Rack.
1. Informations générales
Lors de la fabrication d'un lot de pièces selon le même processus technologique, par le même travailleur, sur le même lieu de travail, dans les mêmes conditions, les écarts des valeurs des paramètres de précision des pièces par rapport au prototype idéal et entre eux sont observé. il phénomènej'ai le nom diffusion.
A tous les stades du processus technologique de fabrication d'une pièce, un grand nombre de facteurs aléatoires et systématiques en évolution continue ou discrète agissent.
Facteurs systématiquesil y a:
- permanent (par exemple, l'erreur de forme de la surface usinée due au non-parallélisme de l'axe de la broche avec les guides de tour; erreur de mesure, etc.);
- changer selon une certaine loi y \u003d f(x) (par exemple, usure dimensionnelle de l'outil, déformation thermique de la machine, etc.).
Facteurs aléatoirescaractérisé par un grand nombre d'entre eux, un manque de communication entre eux et une instabilité (par exemple, des pressions élastiques des liens du système de lutte contre le sida).
En pratique, le phénomène de diffusion de toute caractéristique de qualité est étudié à l'aide d'un nuage de points, qui vous permet de déterminer toutes les caractéristiques.
Pour la construction nuage de pointssur l'axe des abscisses les nombres d'ordonnées des mesures des pièces sont tracés, et sur l'axe des ordonnées sous forme de points - les valeurs obtenues du nombre correspondant de mesures des pièces (Fig. 1.1). A travers les points correspondant aux valeurs de mesure maximale et minimale, deux lignes sont dessinées, parallèles l'une à l'autre et à l'axe des abscisses. La distance entre ces lignes est la première caractéristique de la diffusion des valeurs et est appelée champ de diffusion ω \u003d A nb – UNE nm . Cette caractéristique est nécessairement complétée par la coordonnée du milieu du champ de diffusion - ∆ ω , qui est la distance entre le centre du champ parasite et la valeur nominale. Il détermine la position du champ parasite par rapport à la valeur nominale.
La deuxième caractéristique du phénomène de diffusion est la courbe de diffusion pratique et les paramètres qui la déterminent. Pour construire une courbe de diffusion pratique, un champ de diffusion est nécessaire ω sur un diagramme de dispersion, divisez en 7 ... 11 intervalles par des lignes parallèles à l'axe des abscisses. Dans chaque intervalle, comptez le nombre de résultats de mesure qui y sont tombés (fréquence absolue t)et représenter ce nombre sous forme de rectangles d'une largeur égale à la valeur de l'intervalle et d'une hauteur égale à la fréquence absolue t.
Le diagramme résultant est appelé histogramme de dispersion.En traçant la fréquence absolue tsous la forme de lignes droites situées au milieu de chaque intervalle (ordonnées chargées), et reliant leurs points supérieurs avec des segments de ligne droite, ils obtiennent une ligne brisée appelée courbe de diffusion pratiquevaleurs de mesure (Fig.2.1).
Figure. 1.1. Nuage de points et pratique
courbe de dispersion des valeurs de mesure
Les paramètres caractérisant la courbe de diffusion pratique sont:
1. L'équation de la courbe de diffusion y \u003d φ(x). Pour la plupart des problèmes d'évaluation de la précision dans la technologie du génie mécanique, la distribution des valeurs actuelles x je obéit à la loi normale (loi de Gauss), pour laquelle
En plus de la loi de Gauss, les valeurs actuelles x i peut être distribué selon la loi de probabilité égale, la loi de Simpson, la loi de Charlier, etc.
2. Centre de regroupementd'une variable aléatoire est la valeur moyenne autour de laquelle se situe le plus grand nombre de valeurs. En d'autres termes, le centre de regroupement est la valeur de la variable aléatoire appartenant à la majorité des pièces du lot. La position du centre de regroupement est déterminée par la coordonnée du centre de regroupement (espérance mathématique) M(x).
3. Écart carré moyen σ,affichage de la densité de regroupement des valeurs actuelles par rapport au centre de regroupement M(x). Graphiquement σ représenté par deux abscisses, équidistantes de la valeur M(x) par le montant σ, Cette caractéristique sert de mesure de dispersion.
4. Coefficient d'asymétrie relative a,affichage du décalage du centre de regroupement M(x) par rapport au milieu du champ de diffusion. Pour les valeurs discrètes de la valeur actuelle x je caractéristiques M(x), σ et etsont déterminées par les égalités:
où r(x i) = t / n– le nombre de valeurs de mesure comprises dans l'intervalle correspondant, exprimé en pourcentage ou en fractions du nombre total de valeurs mesurées (fréquence relative).
Les caractéristiques de dispersion calculées des valeurs de mesure sont présentées graphiquement, en tenant compte du fait que à m ax ≈ 0,4 / σ , pour σ ≈0.24/σ (fig. 2.2).
Figure. 2.2. Caractéristiques du phénomène de diffusion: M(x); σ ; et
2. L'ordre de travail
Les travaux de laboratoire sont effectués par deux équipes. Le phénomène de diffusion dans ce travail est étudié sur l'exemple de deux lots de pièces de 50 pièces chacun avec des dénominations ET 1 , ET 2 .
Installez (50 fois) la pièce dans un mandrin à trois mors et mesurez le déplacement axial.
Lors de l'installation, la pièce doit être fermement pressée avec la surface d'extrémité sur l'outillage, et lors d'installations répétées, la pièce doit être tournée autour de son axe selon un certain angle.
Enregistrez les résultats de mesure après chaque installation de la pièce.
Sur la base des résultats de mesure, construisez un nuage de points, un histogramme et une courbe de diffusion similaire à l'étape 2 .
Déterminer les paramètres caractérisant la courbe de diffusion, de manière similaire à l'étape 3 .
Comparez les résultats expérimentaux et tirez des conclusions.
Construisez un diagramme de ces caractéristiques du phénomène de diffusion (Figure 2.2).
1. Nom, but et équipement de l'ouvrage.
2. Les résultats des mesures de pièces par valeur nominale ET 1 .
3. Diagramme de dispersion et caractéristiques du phénomène de diffusion.
4. Résultats des mesures des pièces par valeur nominale ET 2 .
5. Diagramme de dispersion et caractéristiques du phénomène de diffusion.
6. Conclusions.
4. Questions de contrôle
1. Quel est le phénomène de diffusion?
2. Avec l'aide de ce que le phénomène de diffusion est étudié.
3. Nommez les caractéristiques du phénomène de diffusion.
4. Quels sont les facteurs impliqués dans le processus de fabrication d'une pièce?
5. Quels sont les facteurs systématiques responsables dans le nuage de points?
6. Quels sont les facteurs aléatoires responsables dans un nuage de points?
7. Pourquoi le nombre d'intervalles devrait-il être impair lors de la construction d'une courbe de diffusion pratique?
8. Qu'est-ce qu'un champ parasite?
9. Quelle est la coordonnée du milieu du champ de diffusion?
10. Pourquoi la coordonnée du milieu du champ de diffusion est-elle nécessaire?
11. Qu'est-ce qu'un centre de regroupement?
12. Quelle est la valeur attendue?
13. Que montre l'attente mathématique?
14. Qu'est-ce qui est considéré comme une mesure de dispersion?
15. Quelles sont les caractéristiques du déroulement du processus technologique.
16. Quelles sont les caractéristiques du phénomène de diffusion lors du traitement d'un lot de pièces.
Pour une analyse mathématique et statistique des résultats de l'échantillon, il ne suffit pas de connaître uniquement les caractéristiques du poste. La même valeur moyenne peut caractériser des échantillons complètement différents.
Par conséquent, en plus d'eux, les statistiques sont également prises en compte caractéristiques de diffusion (variations, ou fluctuations ) résultats.
1. Portée de la variation
Définition. Dans un balayage la variation est la différence entre les résultats de l'échantillon le plus grand et le plus petit, notée R et est déterminé
R=X max - X min.
La valeur informative de cet indicateur n'est pas élevée, bien qu'avec des échantillons de petite taille en termes de fourchette, il soit facile d'évaluer la différence entre les meilleurs et les pires résultats des athlètes.
2. Dispersion
Définition. Dispersion est appelé le carré moyen de l'écart des valeurs de l'attribut par rapport à la moyenne arithmétique.
Pour les données non groupées, la variance est déterminée par la formule
où X je - la valeur de la fonctionnalité,  - moyen.
- moyen.
Pour les données regroupées en intervalles, la variance est déterminée par la formule
 ,
,
où x je - moyenne je intervalle de regroupement, n je - fréquence des intervalles.
Pour simplifier les calculs et éviter les erreurs de calcul lors de l'arrondissement des résultats (en particulier lors de l'augmentation de la taille de l'échantillon), d'autres formules sont également utilisées pour déterminer la variance. Si la moyenne arithmétique a déjà été calculée, la formule suivante est utilisée pour les données non groupées:
2 \u003d  ,
,
pour les données groupées:
 .
.
Ces formules sont obtenues à partir des précédentes en révélant le carré de la différence sous le signe somme.
Dans les cas où la moyenne arithmétique et la variance sont calculées simultanément, les formules sont utilisées:
pour les données non groupées:
2 \u003d  ,
,
pour les données groupées:
 .
.
3. Carré moyen(la norme) déviation
Définition. Carré moyen racine (la norme ) déviation caractérise le degré d'écart des résultats par rapport à la moyenne en unités absolues, car, contrairement à la variance, il a les mêmes unités de mesure que les résultats de mesure. En d'autres termes, l'écart type indique la densité de distribution des résultats dans un groupe autour de la moyenne, ou l'homogénéité du groupe.
Pour les données non groupées, l'écart type peut être déterminé à l'aide des formules
=  ,
,
=  ou \u003d
ou \u003d  .
.
Pour les données regroupées en intervalles, l'écart type est déterminé par les formules:
 ,
,
 ou
ou  .
.
4. Erreur moyenne arithmétique (erreur moyenne)
Erreur moyenne arithmétique caractérise l'oscillation de la moyenne et est calculée par la formule:
 .
.
Comme le montre la formule, avec une augmentation de la taille de l'échantillon, l'erreur de la moyenne diminue proportionnellement à la racine carrée de la taille de l'échantillon.
5. Coefficient de variation
Le coefficient de variation est défini comme le rapport de l'écart type à la moyenne arithmétique, exprimé en pourcentage:
 .
.
On pense que si le coefficient de variation ne dépasse pas 10%, alors l'échantillon peut être considéré comme homogène, c'est-à-dire obtenu à partir d'une population générale.
Outre la valeur de risque la plus probable, la répartition des valeurs possibles du risque par rapport à sa valeur centrale est importante. La prise en compte de la diffusion des indicateurs est également nécessaire pour résoudre les problèmes de suivi social et hygiénique.
Les caractéristiques les plus courantes de la dispersion d'une variable aléatoire sont la variance et l'écart type.
La variance de la variable aléatoire ξ notée ré (ξ) (nous utilisons également la notation V (ξ) et σ 2 (ξ)), caractérise la valeur la plus probable du carré de l'écart d'une variable aléatoire par rapport à son espérance mathématique.
Pour une variable aléatoire discrète prenant des valeurs x i avec probabilités p i, la variance est définie comme la somme pondérée des écarts de nitrate x i sur l'espérance mathématique ξ avec des coefficients de pondération égaux aux probabilités correspondantes:
D (ξ) \u003d
Pour une variable aléatoire continue ξ, sa variance est déterminée par la formule:
D (ξ) \u003d
La dispersion a les propriétés pratiquement importantes suivantes:
1. La variance de toute variable aléatoire est non négative:
D (ξ) ≥ 0
2. La variance de la constante est 0:
D (C) \u003d 0
où C est une constante.
3. La variance d'une variable aléatoire ξ est égale à la différence entre l'espérance mathématique du carré de cette variable aléatoire et le carré de l'espérance mathématique ξ:
D (ξ) \u003d M [ξ - M (ξ)] 2 \u003d M (ξ 2) - ( .
4. L'ajout d'une constante à une variable aléatoire ne change pas la variance; la multiplication d'une variable aléatoire par une constante a conduit à multiplier la variance par un 2 :
D (aξ + b) \u003d a 2 D (ξ),
où et et b - constantes.
5. La variance de la somme des variables aléatoires indépendantes est égale à la somme de leurs variances:
où ξ et η sont des variables aléatoires indépendantes.
L'écart type d'une variable aléatoire ξ (le terme «écart type» est également utilisé) est le nombre σ (ξ) égal à la racine carrée de la variance ξ:
L'écart type mesure l'écart d'une variable aléatoire par rapport à son espérance mathématique dans les mêmes quantités dans lesquelles la variable aléatoire elle-même est mesurée (par opposition à la variance, dont la dimension est égale au carré de la dimension de la variable aléatoire d'origine) . Pour une distribution normale, l'écart type est égal au paramètre σ. Ainsi, l'espérance mathématique et l'écart type représentent un ensemble complet de caractéristiques de la distribution normale et déterminent de manière unique la forme de la densité de distribution. Pour les distributions autres que la normale, cette paire d'indicateurs n'est pas une caractéristique tout aussi efficace de la distribution.
Le coefficient de variation est également utilisé comme caractéristique de la diffusion d'une variable aléatoire. Le coefficient de variation d'une variable aléatoire ξ avec espérance mathématique non nulle est le nombre V (ξ) égal au rapport de l'écart type ξ à son espérance mathématique:
Le coefficient de variation mesure la dispersion d'une variable aléatoire en fractions de son espérance mathématique et est souvent exprimé en pourcentage de cette dernière. Cette caractéristique ne doit pas être utilisée si l'espérance mathématique est proche de 0 ou significativement inférieure à l'écart type (dans ce cas, de petites erreurs dans la détermination de l'espérance mathématique conduisent à une erreur élevée pour le coefficient de variation), et aussi si la forme de la densité de distribution diffère significativement de Gaussian.
Coefficient d'asymétrie ( Comme) détermine le 3ème degré d'écart d'une variable aléatoire par rapport à l'espérance mathématique et est déterminé par la formule:
En pratique, cet indicateur est utilisé comme une estimation de la symétrie de la distribution. Pour toute distribution symétrique, elle est égale à 0. Si la densité de distribution est asymétrique (ce qui peut souvent être le cas lors de l'évaluation du risque de décès et des risques liés à la pollution de l'eau et de l'air), alors un coefficient d'asymétrie positif correspond au cas où l'épaule gauche de la courbe de densité est plus raide que celle de droite et négative - lorsque l'épaule droite est plus raide que la gauche (figure 4.17).
Pour les distributions asymétriques, l'écart type n'est pas un bon indicateur de la dispersion d'une variable aléatoire. Pour caractériser la diffusion dans ce cas, vous pouvez utiliser des indicateurs tels que des quartiles, des quantiles et des centiles.
Le premier quartile d'une variable aléatoire ξ avec une fonction de distribution F (x) est le nombre Q 1 qui est une solution à l'équation
F (Q 1) \u003d 1/4
c'est-à-dire un nombre pour lequel la probabilité que ξ prenne des valeurs inférieures à Q 1, est égal à 1/4, la probabilité qu'il prenne des valeurs supérieures à Q 1est égal à 3/4.
Le deuxième quartile ( Q 2) d'une variable aléatoire est appelée sa médiane, et la troisième ( Q 3) est la solution de l'équation
F (Q 3) \u003d 3/4
Les quartiles divisent l'axe des abscisses en 4 intervalles: [-∞, Q 1], [Q 1, Q 2], [Q 2, Q 3] et [ Q 3, + ∞] dans chacun desquels la variable aléatoire tombe avec une probabilité égale, et le chiffre délimité par l'axe des abscisses et le graphique de densité de distribution - en 4 zones de même surface. Et l'intervalle entre le premier et le troisième quartiles contient 50% de la distribution de la variable aléatoire. Pour les distributions symétriques, les premier et troisième quartiles sont également éloignés de la médiane.
Quantile d'ordre r d'une variable aléatoire ξ avec une fonction de distribution F (x) est le nombre xqui est une solution à l'équation
Ainsi, les quartiles sont des quantiles de l'ordre de 0,25, 0,5 et 0,75. Si l'ordre quantile p est exprimé en pourcentage, alors les valeurs correspondantes x sont appelés centiles, ou r-pourcentage de points de distribution.
En figue. 4.18 montre, avec les quantiles, des points de distribution de 2,5 et 97,5%. Entre ces points, 95% de la distribution d'une variable aléatoire est concentrée, par conséquent, l'intervalle entre eux est appelé l'intervalle de confiance à 95% de la moyenne (en particulier, lors de l'évaluation des risques - l'intervalle de confiance à 95% du risque).
Objectif 2. Laquelle des informations suivantes sur la variable aléatoire ξ nous permet de rejeter l'hypothèse selon laquelle elle est distribuée selon la loi normale:
a) ξ est une variable aléatoire discrète;
b) l'espérance mathématique ξ est négative;
c) la distribution de ξ est unimodale;
d) l'espérance mathématique ξ n'est pas égale à sa médiane;
e) le coefficient d'asymétrie ξ est négatif;
f) l'écart type ξ est supérieur à son espérance mathématique;
g) ξ caractérise la répartition de la durée des maladies respiratoires aiguës dans la zone d'étude;
h) ξ caractérise la distribution de l'espérance de vie dans la zone d'étude;
i) la médiane ξ ne coïncide pas avec le centre de l'intervalle entre les premier et troisième quartiles.
Réponse: L'hypothèse concernant la distribution normale d'une variable aléatoire est incompatible avec les énoncés a), d), e), h) et i).
Figure. 4.17.Dépendance entre signe Graphique 4.18. Quartiles et centiles:
illustration du coefficient d'asymétrie et de la forme à l'aide de la fonction
fonctions de densité de distribution